- Sparking a Sense of Wonder to elicit students’ innate curiosities and thinking
- Powerful Math and Science ideas at the core of each lesson
- Revising and refining ideas through Modeling Activities
- Pressing students for justification and sense-making




Parallel Processes used in Math and Science Integrated PBL
| Mathematical Modeling | Scientific Modeling | |
| Spark a sense of Wonder |
Posing the Problem Statement: Is it real-world and does it require math modeling? What mathematical questions come to mind? |
The first quality of “models for modeling” is that they should represent an event or process (we often use the term “phenomenon” for this), rather than “things.” |
| Research |
Making Assumptions to Define, and Simplify the Real World Problem: What assumptions do you make? What are the constraints that help you define and simplify the problem? Considering the Variables: What variables will you consider? What data/information is necessary to answer your question? |
The phenomenon should be context-rich, meaning that it is about a specific event that happens in a specific place and time under specific conditions. These “specifics” are precisely what make the models interesting to students.
|
| Explore |
Be the Mathematician. Building solutions, making conjectures, testing and refining their mathematical model using tools and the mathematics that students bring as prior knowledge and seek new knowledge that can help them understanding the phenomenon in the real world. |
Be the Scientist-Asking questions, designing studies, collecting and analyzing data, arguing about evidence, and communicating findings. Students’ models may be pictorial, visual resemblance between the representations on paper and the process or event being modeled. |
| Revise |
Analyzing and Validating their Conclusions: Does your solutions make sense? Now, take your solution and apply it to the real world scenario. How does it fit? What do you want to revise? Presenting and Justifying the Reasoning for Your Solution. |
The final quality of models for modeling is that they are revisable. Because models show how events, things, properties and ideas are related to one another, students need to test these relationships out. As a result of readings, activities, discussions, and experiments, students make changes to their models over time. |
Developing and Using Models
Below is the progression of the Science and Engineering Practice of Developing and Using Models, followed by Performance Expectations that make use of this Science and Engineering Practice.
Developing and Using Models
A practice of both science and engineering is to use and construct models as helpful tools for representing ideas and explanations. These tools include diagrams, drawings, physical replicas, mathematical representations, analogies, and computer simulations.
Primary School (K-2)
Distinguish between a model and the actual object, process, and/or events the model represents.
Compare models to identify common features and differences.
Develop and/or use a model to represent amounts, relationships, relative scales (bigger, smaller), and/or patterns in the natural and designed world(s).
Develop a simple model based on evidence to represent a proposed object or tool.
Elementary School (3-5)
Identify limitations of models.
Collaboratively develop and/or revise a model based on evidence that shows the relationships among variables for frequent and regular occurring events.
Develop a model using an analogy, example, or abstract representation to describe a scientific principle or design solution.
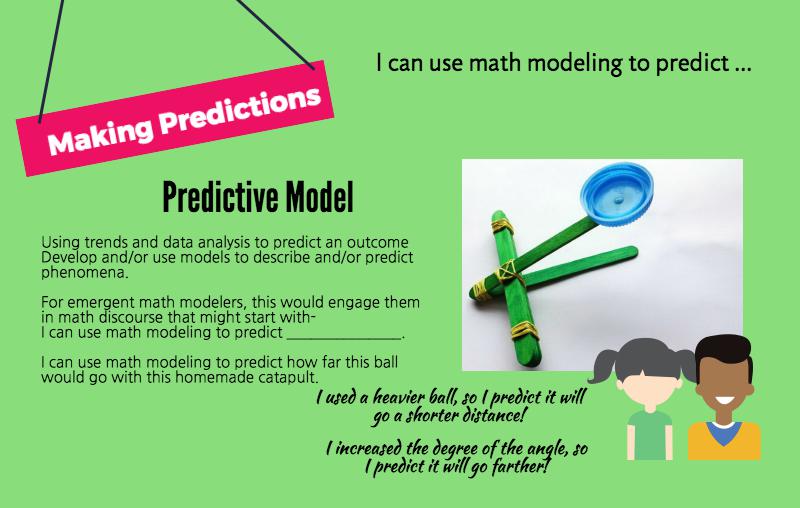
Develop and/or use models to describe and/or predict phenomena.
Develop a diagram or simple physical prototype to convey a proposed object, tool, or process.
Use a model to test cause and effect relationships or interactions concerning the functioning of a natural or designed system.
Middle School (6-8)
Evaluate limitations of a model for a proposed object or tool.
Develop or modify a model—based on evidence – to match what happens if a variable or component of a system is changed.
Use and/or develop a model of simple systems with uncertain and less predictable factors.
Develop and/or revise a model to show the relationships among variables, including those that are not observable but predict observable phenomena.
Develop and/or use a model to predict and/or describe phenomena.
Develop a model to describe unobservable mechanisms.
Develop and/or use a model to generate data to test ideas about phenomena in natural or designed systems, including those representing inputs and outputs, and those at unobservable scales.
Cross cutting themes
THE THREE DIMENSIONS OF THE FRAMEWORK
SPARK STEM Practices
1. Asking questions and defining problems for Modeling
2. Developing and using models
3. Planning and carrying out investigations
4. Analyzing and interpreting data
5. Using mathematics and computational thinking
6. Constructing models with explanations and designing solutions
7. Engaging in argument from evidence, justifying reasoning
8. Obtaining, evaluating, and communicating information
Crosscutting Concepts
1. Patterns
2. Cause and effect: Mechanism and explanation
3. Scale, proportion, and quantity
4. Systems and system models
5. Energy and matter: Flows, cycles, and conservation
6. Structure and function
7. Stability and change
Disciplinary Core Ideas
Science
Mathematics

